Los errores son frecuentes en la informática, ya sean producidos por el software, o por el hardware. En éste último caso, cuando un bit cambia de valor, puede afectar enormemente a los resultados, produciendo valores incorrectos. Por eso, para ciertas aplicaciones críticas, se utiliza la corrección de errores, un concepto que vamos a introducir en este artículo.
¿Qué es la corrupción de datos?
La corrupción de datos no es más que los errores que afectan a la integridad de los datos binarios durante su transmisión o cuando se intenta acceder a ellos, llevando a cambios no deseados en los datos originales. Por ejemplo, los datos almacenados en un disco duro pueden corromperse debido a factores externos, como impactos causados por sismos, que resultan en daños físicos al medio de almacenamiento. También puede ocurrir por otros factores, como fallos en los sectores del disco, malware, cortes repentinos de electricidad, apagar o desconectar de forma no segura el dispositivo, etc.
Esta corrupción de datos lleva a la pérdida de datos, lo cual es un gran problema en una sociedad tan dependiente de los datos como la actual. Por tanto, hay que aplicar medidas para evitar estas pérdidas, como son los métodos de corrección de errores que más adelante explicaré.
¿Corrección de errores?
La corrección de errores se refiere a la identificación, análisis y solución de defectos en software o sistemas informáticos. Puede manifestarse como fallos, comportamientos inesperados, resultados incorrectos o bloqueos. Es esencial en el desarrollo y mantenimiento de software y sistemas. Se detecta un error, se depura para hallar la causa, implicando revisión de código, pruebas y herramientas diagnósticas. Luego, se corrige el error mediante cambios en código, configuración, parches o actualizaciones. Se hacen pruebas para confirmar la solución y evitar nuevos problemas.
Algunas técnicas solo implican corrección de errores, es decir, solo se limitan a detectarlos, pero no a corregirlos.
Además, la corrección no se limita al software; también abarca hardware, identificando y reparando problemas físicos en componentes como discos duros o memoria RAM (véase ECC), etc., como explicaré en el siguiente apartado
Aplicaciones
Algunos usos y aplicaciones de los sistemas de corrección de errores son:
- Niveles de control de errores en TCP/IP: La corrección de errores en una pila TCP/IP se realiza a través de diferentes métodos, como detección de errores CRC-32 en tramas Ethernet, sumas de control en encabezados IPv4 e IPv6, y sumas de verificación en UDP y TCP. En el caso de TCP, se retransmiten paquetes con sumas incorrectas.
- Telecomunicaciones en el espacio profundo: El desarrollo de códigos de corrección de errores se vincula a misiones espaciales por la debilitación de la señal y la limitada energía. Se usaron códigos convolucionales y Reed-Muller, y las misiones Voyager utilizaron códigos más complejos para transmitir datos científicos. Actualmente, se recomienda códigos como el RSV de Voyager 2.
- Radiodifusión por satélite: La demanda de ancho de banda por satélite crece debido a la transmisión de televisión y datos IP. Los códigos de corrección de errores son esenciales para mejorar la fiabilidad y eficiencia del ancho de banda en los transpondedores.
- Almacenamiento de datos: Los códigos de detección y corrección de errores se utilizan en medios de almacenamiento, como cintas magnéticas y discos duros, para detectar y corregir errores de lectura. También se usan en sistemas RAID para recuperar datos en caso de fallo de un disco duro.
- Memoria con corrección de errores: En las memorias DRAM, se usan códigos de corrección de errores para detectar y corregir errores suaves. Esto es crucial para aplicaciones críticas y en entornos de alta radiación, como el espacio. Los controladores de memoria y sistemas operativos también participan en la detección y corrección de errores.
Tipos de corrección de errores
Existen varios métodos de corrección de errores que deberías conocer, y los más importantes y usados en la actualidad son:
El bit de paridad es un método simple de detección de errores en la transmisión de datos. Funciona agregando un bit adicional, conocido como «bit de paridad», a un conjunto de bits de datos. El objetivo principal del bit de paridad es detectar errores en la transmisión, especialmente cuando se transmiten datos en canales ruidosos o propensos a errores.
Existen dos tipos principales de bits de paridad:
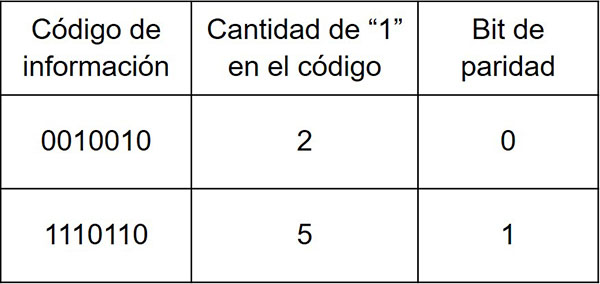
- Paridad Par: en este método, se suma la cantidad de unos (bits con valor 1) en el conjunto de bits de datos, incluyendo el bit de paridad. Si la cantidad total de unos es par, el bit de paridad se establece en 0 para que el total de unos sea par. Si la cantidad de unos es impar, el bit de paridad se establece en 1 para que el total sea par. Al recibir los datos, el receptor vuelve a contar los unos en el conjunto y compara el resultado con el bit de paridad recibido. Si no coinciden, se asume que ha ocurrido un error durante la transmisión.
- Paridad Impar: se realiza un proceso similar al de la paridad par, pero en lugar de hacer que la cantidad total de unos sea par, se hace que sea impar. Si la cantidad total de unos es impar, el bit de paridad se establece en 0 para que el total de unos sea impar. Si la cantidad de unos es par, el bit de paridad se establece en 1 para que el total sea impar. Al igual que en la paridad par, el receptor compara el bit de paridad recibido con el recuento de unos en el conjunto de bits para detectar errores.
Por ejemplo: imagina que se tiene que transmitir o acceder a un byte de datos que es el siguiente: 0110010. Si usamos el bit de paridad par, lo calculamos de la siguiente forma:
- Contamos la cantidad de bits que son uno en este byte, que en este caso son 3.
- La cantidad de unos es impar, al ser 3, por lo que el bit de paridad es el 1.
- Ya tenemos que que nuestro byte es 0110010 y el bit de paridad es 1, por lo que será 01100101.
- Imagina que el bit de la posición 5 se cambia de 0 a 1 por un error. Y entonces el byte se queda 01101101.
- Como habíamos calculado la cantidad de unos con el bit de paridad y debía ser un número impar (3) y ahora tenemos 4 unos, par, al comprobar el byte sabremos que ha habido un error.
En este ejemplo, el bit de paridad logra detectar el error causado por la corrupción de datos durante la transmisión. Es importante destacar que este método puede detectar errores, pero no puede corregirlos. Para aplicaciones más avanzadas, se utilizan técnicas de detección y corrección de errores más sofisticadas. Además, si el bit corrupto es el de paridad, entonces tampoco servirá de nada, como tampoco serviría si hay cambio en más de un bit y el resultado es igual al bit de paridad marcado…
Checksum o suma de verificación
La suma de verificación, también conocida como checksum en inglés, es un método utilizado para verificar la integridad de datos durante la transmisión, almacenamiento o recepción. Consiste en generar un valor numérico o un conjunto de bits a partir de los datos originales, de manera que cualquier cambio en los datos resulte en un valor de suma de verificación diferente. Al comparar la suma de verificación calculada con la que se recibe o se tiene previamente, es posible detectar si ha ocurrido algún error o corrupción en los datos. Seguro que has usado este método cuando descargas alguna ISO de un sistema operativo y la tienes que comprobar mediante algoritmos como MD5, SHA1, etc.
Para verlo de una forma más sencilla, voy a poner un ejemplo: imagina que se desea transmitir la palabra HOLA! y que se quiere comprobar si se ha transmitido o leído de forma correcta mediante checksum. Entonces tenemos:
- Palabra original: HOLA!
- Cálculo de la suma de verificación usando el valor ASCII en binario y determinando la cantidad de unos para ver si es par o impar la paridad.
- H (7 en ASCII) –> 01001000 (Cantidad de unos: 2)
- O (79 en ASCII) –> 01001111 (Cantidad de unos: 4)
- L (76 en ASCII) –> 01001100 (Cantidad de unos: 2)
- A (65 en ASCII) –> 01000001 (Cantidad de unos: 2)
- ! (33 en ASCII) –> 00100001 (Cantidad de unos: 2)
- Tenemos que la paridad total en este caso es 2+4+2+2+2=12 (esa es la cantidad total de bits a 1).
- Los datos transmitidos serían HOLA!.
- Imagina que durante la transmisión se pierde el segundo carácter y se queda como HELA!. Es decir, se ha perdido la O y se ha cambiado por una E.
- Al recibir los datos, el receptor realiza el mismo cálculo de suma de verificación. Si el resultado no coincide con la suma, habrá un error en el checksum y se habrá detectado el fallo. En este caso, la suma de verificación no sería 12, la E (69 en ASCII) corresponde al binario 01000101 (Cantidad de unos: 3). Por tanto, la suma total sería 11.
Evidentemente este es un ejemplo muy sencillo, las sumas se realizan mediante complejos algoritmos.
Código Hamming
El código de Hamming es un tipo de código de detección y corrección de errores utilizado en la transmisión y almacenamiento de datos. Fue desarrollado por Richard W. Hamming en la década de 1950 y se utiliza para detectar y corregir errores en los datos transmitidos o almacenados. El código de Hamming agrega bits de paridad adicionales a los datos para permitir la detección y, en algunos casos, la corrección de errores.
Un ejemplo para comprender mejor este método de corrección de errores sería imaginar que se quiere trasnsmitir el código 1011. Son 4-bits, pero con el código Hamming vamos a agregar 3 bits adicionales de paridad, por lo que quedaría como un número de 7-bits.
- Primero hay que calcular los bits de paridad, que en este caso estarán en las posiciones que son potencias de 2 (1, 2, 4, 8,…). Como en este caso tenemos 7-bits, tendríamos en las posiciones 1, 2 y 4.
- Si el conteo es par será 0 el bit de paridad, y si es impar será 1. En este caso tenemos lo siguiente:
- Bit de Paridad P1: Cubre las posiciones 1, 3, 5, 7. (1 + 0 + 1 + 1) = 3 (impar)
- Bit de Paridad P2: Cubre las posiciones 2, 3, 6, 7. (0 + 0 + 1 + 1) = 2 (par)
- Bit de Paridad P4: Cubre las posiciones 4, 5, 6, 7. (1 + 1 + 1 + 1) = 4 (par)
- Los bits de paridad calculados son: P1 = 1, P2 = 0, P4 = 0.
- El código Hammimng completo sería P1P2X1P4X2X3X4 (7 bits).
- Suponiendo que durante la transmisión el bit de la posición 3 (X1) conmuta y cambia de 1 a 0, entonces los datos recibidos sería diferente al calculado anteriormente.
- Entonces se produce un error y se sabe que el valor no es correcto.